This is the first post I’ve written in a while. I have been somewhat radio silent on social media, but I’m jumping back in.
Now, I work with brain images, which can have millions of elements (referred to as voxels). Many of these elements are zero (for background). We want to calculate basic statistics on the data usually and I wanted to describe how you can speed up operations or reduce memory requirements if you want to calculate many statistics on a large vector with integer values by using summary tables.
Why to use Tables
Tables are relatively computationally expensive to calculate. They must operate over the entire vector, find the unique values, and bin the data into these values. Let 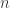 be the length of the vector. For integer vectors (i.e. whole number), the number of unique values is much less than
be the length of the vector. For integer vectors (i.e. whole number), the number of unique values is much less than 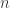 . Therefore, the table is stored much more efficiently than the entire vector.
. Therefore, the table is stored much more efficiently than the entire vector.
Tables are sufficient statistics
You can think of the frequencies and bins as summary statistics for the entire distribution of the data. I will not discuss a formal proof here, but you can easily re-create the entire vector using the table (see epitools::expand.table for a function to do this), and thus the table is a sufficient (but not likely a minimal) statistic.
As a sufficient statistic, we can create any statistic that we’d like relatively easy. Now, R has very efficient functions for many statistics, such as the median and quantiles, so it may not make sense why we’d want to rewrite some of these functions using tables.
I can think of 2 reasons: 1) you want to calculate many statistics on the data and don’t want to pass the vector in multiple times, and 2) you want to preprocess the data to summarize the data into tables to only use these in memory versus the entire vector.
Here are some examples when this question has been asked on stackoverflow: 1, 2 and the R list-serv: 1. What we’re going to do is show some basic operations on tables to get summary statistics and show they agree.
R Implementation
Let’s make a large vector:
set.seed(20150301)
vec = sample(-10:100, size= 1e7, replace = TRUE)
Quantile function for tables
I implemented a quantile function for tables (of only type 1). The code takes in a table, creates the cumulative sum, extracts the unique values of the table, then computes and returns the quantiles.
quantile.table = function(tab, probs = c(0, 0.25, 0.5, 0.75, 1)){
n = sum(tab)
#### get CDF
cs = cumsum(tab)
### get values (x)
uvals = unique(as.numeric(names(tab)))
# can add different types of quantile, but using default
m = 0
qs = sapply(probs, function(prob){
np = n * prob
j = floor(np) + m
g = np + m - j
# type == 1
gamma = as.numeric(g != 0)
cs <= j
quant = uvals[min(which(cs >= j))]
return(quant)
})
dig <- max(2L, getOption("digits"))
names(qs) <- paste0(if (length(probs) < 100)
formatC(100 * probs, format = "fg", width = 1, digits = dig)
else format(100 * probs, trim = TRUE, digits = dig),
"%")
return(qs)
}
Quantile Benchmarks
Let’s benchmark the quantile functions: 1) creating the table and then getting the quantiles, 2) creating an empircal CDF function then creating the quantiles, 3) creating the quantiles on the original data.
library(microbenchmark)
options(microbenchmark.unit='relative')
qtab = function(vec){
tab = table(vec)
quantile.table(tab)
}
qcdf = function(vec){
cdf = ecdf(vec)
quantile(cdf, type=1)
}
# quantile(vec, type = 1)
microbenchmark(qtab(vec), qcdf(vec), quantile(vec, type = 1), times = 10L)
Unit: relative
expr min lq mean median uq
qtab(vec) 12.495569 12.052644 9.109178 11.589662 7.499691
qcdf(vec) 5.407606 5.802752 4.375459 5.553492 3.708795
quantile(vec, type = 1) 1.000000 1.000000 1.000000 1.000000 1.000000
max neval cld
5.481202 10 c
2.653728 10 b
1.000000 10 a
More realistic benchmarks
Not surprisingly, simply running quantile on the vector beats the other 2 methods, by far. So computational speed may not be beneficial for using a table. But if tables or CDFs are already created in a previous processing step, we should compare that procedure:
options(microbenchmark.unit="relative")
tab = table(vec)
cdf = ecdf(vec)
all.equal(quantile.table(tab), quantile(cdf, type=1))
[1] TRUE
all.equal(quantile.table(tab), quantile(vec, type=1))
[1] TRUE
microbenchmark(quantile.table(tab), quantile(cdf, type=1), quantile(vec, type = 1), times = 10L)
Unit: relative
expr min lq mean median uq
quantile.table(tab) 1.000 1.000 1.0000 1.000 1.0000
quantile(cdf, type = 1) 774.885 1016.172 596.3217 1144.063 868.8105
quantile(vec, type = 1) 1029.696 1122.550 653.2146 1199.143 910.3743
max neval cld
1.0000 10 a
198.1590 10 b
206.5936 10 b
As we can see, if you had already computed tables, then you get the same quantiles as performing the operation on the vector, and also much faster results. Using quantile on a ecdf object is not much better, which mainly is due to the fact that the quantile function remakes the factor and then calculate quantiles:
stats:::quantile.ecdf
function (x, ...)
quantile(evalq(rep.int(x, diff(c(0, round(nobs * y)))), environment(x)),
...)
<bytecode: 0x107493e28>
<environment: namespace:stats>
Median for tables
Above we show the quantile.table function, so the median function is trivial where probs = 0.5:
median.table = function(tab){
quantile.table(tab, probs = 0.5)
}
Mean of a table
Other functions can be used to calculate statstics on the table, such as the mean:
mean.table = function(tab){
uvals = unique(as.numeric(names(tab)))
sum(uvals * tab)/sum(tab)
}
mean.table(tab)
[1] 44.98991
mean(tab)
[1] 44.98991
mean(cdf)
Warning in mean.default(cdf): argument is not numeric or logical:
returning NA
[1] NA
As we see, we can simply use mean and do not need to define a new function for tables.
mean(vec)
[1] 44.98991
all.equal(mean(tab), mean(vec))
[1] TRUE
Subsetting tables
One problem with using mean vs. mean.table is when you subset the table or perform an operation that causes it to lose the attribute of the class of table. For example, let’s say I want to estimate the mean of the data for values  :
:
mean(vec[vec > 0])
[1] 50.50371
over0 = tab[as.numeric(names(tab)) > 0]
mean(over0)
[1] 90065.98
mean.table(over0)
[1] 50.50371
class(over0)
[1] "array"
We see that after subsetting, over0 is an array and not a table, so mean computes the mean using the array method, treating the frequences as data and the estimated mean is not correct. mean.table calculates the correct value, as it does not depend on the class of tab. Another way to circumvent this is to reassign a class of table to over0:
class(over0) = "table"
mean(over0)
[1] 50.50371
This process requires the user to know what the class is of the object passed to mean, and may not be correct if the user changes the class of the object.
Aside on NA values
Let’s see what happens when there are NAs in the vector. We’ll put in 20 NA values:
navec = vec
navec[sample(length(navec), 20)] = NA
natab = table(navec, useNA="ifany")
nacdf = ecdf(navec)
mean(navec)
[1] NA
mean(natab)
[1] NA
# mean(nacdf)
We see that if we table the data with NA being a category, then any operation that returns NA if NA are present will return NA. For example, if we do a table on the data with the table option useNA="always", then the mean will be NA even though no NA are present in the original vector. Also, ecdf objects do not keep track of NA values after they are computed.
tab2 = table(vec, useNA="always")
mean(tab2)
[1] NA
nonatab = table(navec, useNA="no")
mean(nonatab)
[1] 44.98993
mean(navec, na.rm=TRUE)
[1] 44.98993
If you are using tables for statistics, the equivalent of na.rm=FALSE is table(..., useNA="ifany") and na.rm=TRUE is table(..., useNA="no"). We also see that an object of ecdf do not ever show NAs. Although we said tables are sufficient statistics, that may not be entirely correct if depending on how you make the table when the data have missing data.
Mean benchmark
Let’s benchmark the mean function, assuming we have pre-computed the table:
options(microbenchmark.unit="relative")
microbenchmark(mean(tab), mean(vec), times = 10L)
Unit: relative
expr min lq mean median uq max neval cld
mean(tab) 1.0000 1.0000 1.0000 1.0000 1.0000 1.00000 10 a
mean(vec) 374.0648 132.3851 111.2533 104.7355 112.7517 75.21185 10 b
Again, if we have the table pre-computed, then estimating means is much faster using the table.
Getting standard deviation
The mean example may be misleading when we try sd on the table:
sd(vec)
[1] 32.04476
sd(tab)
[1] 302.4951
This are not even remotely close. This is because sd is operating on the table as if it were a vector and not a frequency table.
Note, we cannot calculate sd from the ecdf object:
sd(cdf)
Error in as.double(x): cannot coerce type 'closure' to vector of type 'double'
SD and Variance for frequency table
We will create a function to run sd on a table:
var.table = function(tab){
m = mean(tab)
uvals = unique(as.numeric(names(tab)))
n = sum(tab)
sq = (uvals - m)^2
## sum of squared terms
var = sum(sq * tab) / (n-1)
return(var)
}
sd.table = function(tab){
sqrt(var.table(tab))
}
sd.table(tab)
[1] 32.04476
We create the mean, get the squared differences, and sum these up (sum(sq * tab)) , divide by n-1 to get the variance and the sd is the square root of the variance.
Benchmarking SD
Let’s similarly benchmark the data for sd:
options(microbenchmark.unit="relative")
microbenchmark(sd.table(tab), sd(vec), times = 10L)
Unit: relative
expr min lq mean median uq max neval
sd.table(tab) 1.0000 1.0000 1.000 1.000 1.0000 1.0000 10
sd(vec) 851.8676 952.7785 847.225 1142.225 732.3427 736.2757 10
cld
a
b
Mode of distribution
Another statistic we may want for tabular data is the mode. We can simply find the maximum frequency in the table. The multiple option returns multiple values if there is a tie for the maximum frequency.
mode.table = function(tab, multiple = TRUE){
uvals = unique(as.numeric(names(tab)))
ind = which.max(tab)
if (multiple){
ind = which(tab == max(tab))
}
uvals[ind]
}
mode.table(tab)
[1] 36
Memory of each object
We wish to simply show the memory profile for using a table verus the entire vector:
format(object.size(vec), "Kb")
[1] "39062.5 Kb"
format(object.size(tab), "Kb")
[1] "7.3 Kb"
round(as.numeric(object.size(vec) / object.size(tab)))
[1] 5348
We see that the table much smaller than the vector. Therefore, computing and storing summary tables for integer data can be much more efficient.
Conclusion
Tables are computationally expensive. If tables are pre-computed for integer data, however, then statistics can be calculated quickly and accurately, even if NAs are present. These tables are also much smaller in memory so that they can be stored with less space. This may be an important thing to think about computing and storage of large vectors in the future.
